履带式起重性能是各类工程起重设备吊装作业的关键性指导依据之一，其设置的准确及合理性将直接影响起重设备的安全可靠性。就履带起重机而言，起重性能计算需要重点关注臂架强度、整机稳定性及各受力部件性能( 拉板承载能力、变幅能力、单绳拉力、起升倍率) 等因素的综合影响，核算每个限制条件下起重机能够承受的大载荷，从大承受载荷中获取小值作为额定起重性能，形成起重量表。关于履带式起重机设计，不同国家或区域出台了相关设计准则或规

范，如我国的GB 3811—2008《起重机设计规范》、欧洲的EN 13000—2014《起重机移动式起重机》等。探究和解析目前市场成熟产品起重性能存在的分布规律，可为产品研发、改进及工程应用中起重量的预判、规划和掌控提供重要参考。本文对欧美两个品牌履带式起重机系列产品起重量进行分析。首先，通过MATLAB获得欧洲产品起重量数据的变化趋势，进行数据拟合确定函数关系，再通过北美产品进行验证，从而获得可靠性较高的分析结果。

1 起重量分析及评价

1． 1 起重量分析

     选用欧洲某履带起重机系列产品起重量作为基础进行分析，包括100 t、200 t( 中小吨位) 、300 t、400 t( 中吨位) 、500 t、600 t( 中大吨位) 等系列产品，覆盖了工程领域常用的产品系列。下面以100 t 产品主臂工况起重量说明分析过程。欧洲某品牌100 t 履带起重机主臂起重量见表1。

表1 欧洲某品牌100 t 履带起重机主臂起重量表( 部分) t作业幅( m)臂长( m)

    起重量数据分析过程中，以臂长分组将相应作业幅度起重量应用多项式、幂函数、倒幂函数、指数函数、双曲线函数等拟合考察其变化趋势，发现多项式( 式1) 、指数函数( 式2) 、倒幂函数( 式3) 等能够对起重量数据进行较好描述:f( x) = pn•xn + pn － 1•xn － 1… + p1•x + p0 ． ( 1)其中: n 为函数高次数，n = 1，2

，3…; pn为n 次项对应系数。f( x) = a•ebx + c•edx ． ( 2)其中: a、b、c、d 为系数。f( x) = p1 /( x2 + q1•x + q2) ． ( 3)

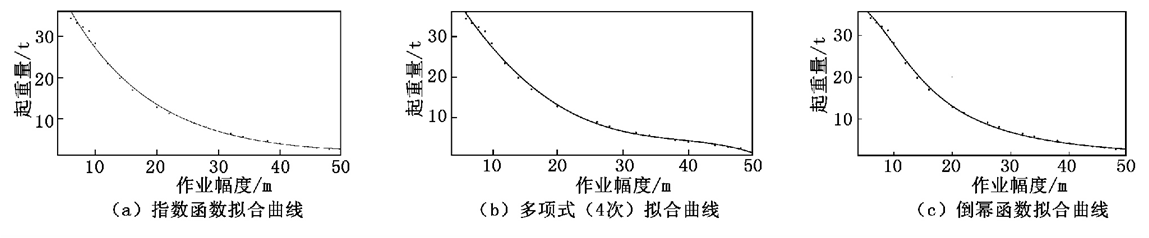
其中: p1、q1、q2为系数。在MATLAB 软件中应用上述三种函数进行数据拟合分析，主要方式有两种: 一种是用函数命令拟合，该法较繁琐; 另一种是用曲线拟合工具包Curve FittingTool 在图形窗口操作，具有简便、快速、可操作性强的优点［2］。本文采用工具包Curve Fitting Tool 进行数据处理，将100 t 产品起重量按不同臂长导入MATLAB软件，采用上述函数逐一进行拟合，可获得每个臂长下起重量随着工作幅度变化的拟合曲线。100 t 履带起重机主臂50 m 的拟合曲线如图1 所示。

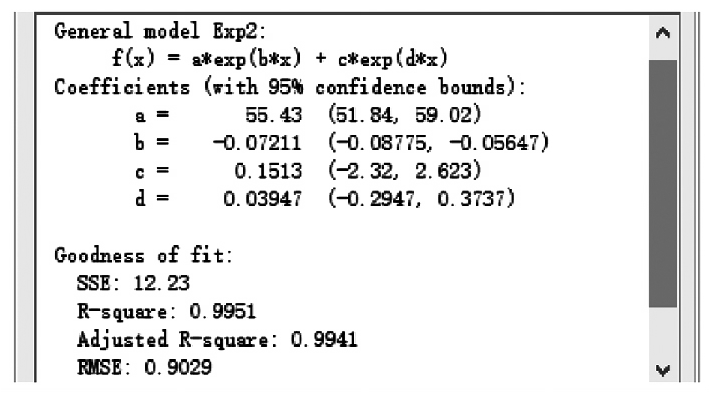
图1 100 t 履带起重机主臂50 m 的拟合曲线图1 显示，对于100 t 履带起重机主臂50 m 工况，指数函数、多项式函数( 4 次) 、倒幂函数均能够较好地逼近起重量随着幅度增大呈现的变化趋势，除10 m 内小幅度起重量与拟合曲线存在偏差，其他起重量均与拟合曲线相近或重合。为表征函数拟合效果，MATLAB 工具包Curve Fitting Tool 提供了评价参数，如图2 所示。

图2 中，上部为指数函数拟合所得系数值，下部为拟合效果评价参数值。图2 曲线拟合工具箱拟合效果评价指标( 100 t 产品主臂50 m)MATLAB 工具包Curve Fitting Tool 提供的评价参数主要包含SSE、Ｒ-square、ＲMSE 等。( 1) SSE( 和方差) : 表征起重量拟合数据和原始数据对应点的误差平方和。其表达式为:SSE =Σmi = 1( yi－ y'i) 2 ． ( 4)其中: yi为原始起重量数据; y'i为拟合起重量数据; m为数据总数量，i = 1，2，3，…，m。SSE 越趋于0，表明

拟合程度与函数选择越佳。

( 2) Ｒ-square ( 确定系数) : Ｒ-square 由误差平方和( 预测数据与原始数据均值之差的平方和) 与标准差( 原始数据和均值之差的平方和) 比值决定。其表达式为:

Ｒ-square = 1 －Σmi =1( yi － y'i) 2 /Σmi =1( yi － ( yi

－ ) ) ． 

( 5)其中: yi－ 为原始起重量均值。Ｒ-square 值正常取值范围为0 ～ 1，比值越趋近1，表明估计值与实际值越接近，数据拟合效果越好。

( 3) ＲMSE( 均方根误差) : 均方根误差对测量数据中特大或特小误差反应敏感，能够很好地反映出测量的精密度。其表达式为:ＲMSE = 1mΣni = 1( yi － y'i) 槡2 ．

 ( 6)表2 和表3 分别为100 t 和400 t 履带起重机起重量( 部分) 采用4 次多项式拟合得到的拟合评价参数。由于履带起重机吨位跨度大，采用数值如SSE 值表征拟合效果时不同吨级履带起重机存在较大差异，如100 t 产品26 m 主臂与400 t 产品28 m 主臂起重量，SSE 值分别为5． 334 和31． 79，但实际上前者Ｒ-square值为0． 999 3 比后者的0． 999 7 还略差。因此，起重量基数的差异可能会使数值型评价参数数值放大，影响评价直观性，故本文后续采用Ｒ-square 值进行评价。表2 100 t 产品起重量( 部分) 拟合评价参数( 4 次多项式)臂长( m) SSE Ｒ-square ＲMSE

表3 400 t 产品起重量( 部分) 拟合评价参数( 4 次多项式)臂长( m) SSE Ｒ-square ＲMSE21

1． 2 起重量拟合评价

按照上述方法，对欧洲某品牌100 t ～ 600 t 系列履带起重机全部起重量进行数据拟合，获得每个产品各臂长Ｒ-square 值，并求取均值及标准差，得到的数据见表4。

其中深色数据为同组中佳数据。表4 欧洲品牌主臂起重量拟合评价参数吨级拟合函数Ｒ-square 值多项式指数函数倒幂函数指标中小吨位中吨位中大吨位

表4 数据显示: ①三种函数均能描述起重量变化趋势，结合Ｒ-square 值可知4 次多项式和指数函数拟合效果更佳;

 ②从吨位级别来看，中小吨位产品4 次多项式拟合数据效果较好，中吨位产品尽管300 t 产品指数函数的Ｒ-square 值佳，但数据离散程度略大，多项式与倒幂函数Ｒ-square 值的均值及标准差相当，综合整体情况可采用4 次多项式进行数据拟合，中大吨位产品指数函数拟合较好。为验证上述结论，选用北美某产品对4 次多项式及指数函数拟合效果进行验证，拟合评价参数见表5。其中深色数据为同组中佳数据，该产品系列中无500 t 产品。

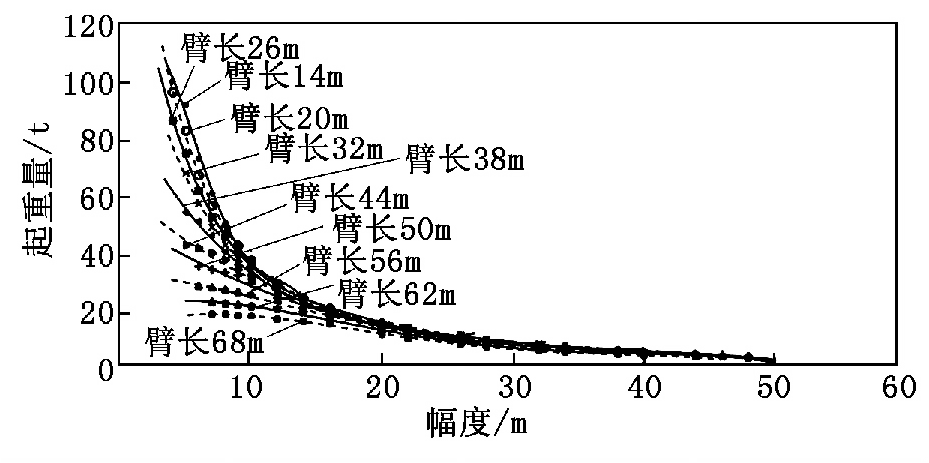
表5 北美某品牌起重机主臂起重量拟合评价参数吨级拟合函数Ｒ-square 均值4 次多项式指数函数中小吨位表5 数据显示，前文结论得到有效验证。综上，中吨位及中小吨位产品可采用4 次多项式描述，中大吨位产品可采用指数函数描述。将表1 中欧洲100 t 产品全部起重量数据绘制散点图并同时绘制每个臂长下起重量4 次多项式拟合曲线，如图3 所示。由图3 可见，起重量按臂长随作业幅度增加依照4 次多项式曲线呈现非线性减小规律。

图3 100 t 起重机起重量散点图及变化规律2 

总结

本文通过对欧美两品牌系列履带起重机起重量进行探析发现，随着作业幅度的增加中吨位及中小吨位产品起重量依照4 次多项式、中大吨位产品起重量依照指数函数曲线呈逐渐减小规律。因此，在履带式起重机设计及工程应用中可以通过4 次多项式及指数函数对起重量进行控制和判断，具有良好的实践指导价值，也为其他工程起重设备起重量的分析提供了思路。

期